Multiple Correspondence Analysis
| Related Online Training modules | |
|---|---|
| Multiple Correspondence Analysis | |
| Generally it is best to access online training from within Q by selecting Help > Online Training |
Multiple Correspondence Analysis is created using the Maps dialog box.
Required data
Pick One, Pick Any and Pick One – Multi questions.
The statistical theory which underlies correspondence analysis assumes that the data is a contingency table created from two Pick One questions. Multiple correspondence can address more than two categorical variables. Whereas correspondence analysis analyzes a table, multiple correspondence analysis analyzes the variables themselves; for example, a Pick Any question with 11 categories is analyzed as 11 categorical variables.
Interpretation
The interpretation of multiple correspondence analysis is the same as for Correspondence Analysis. Often the most useful way of analyzing multiple variables is to use traditional correspondence analysis and not multiple correspondence analysis. This is best understood with an example of analyzing a Pick Any question which contains eleven variables, each measuring whether or not respondents liked particular phone companies.
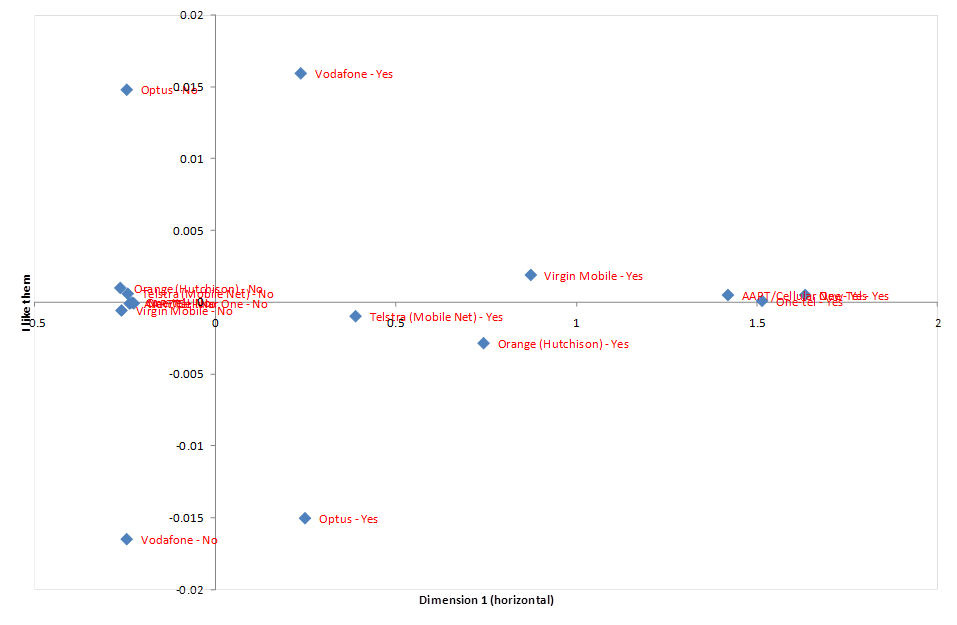
The first thing to note about the output below is that the first dimension is explaining 93.3% of the inertia and the second dimension is explaining 0 (this analysis was conducted using Phone Tidied.Q analyzing the question I like them. Multiple correspondence analysis is essentially a form of principal components analysis for categorical data which has focused on identifying latent variables that explain the data. In particular, it has identified a single latent factor whereby respondents differ in terms of the number of brands that they like.
Total sample
Unweighted
base n = 651
Analysis based on 651 observations (weighted n = 651)
Multiple Correspondence Analysis
Inertia(s):
Canonical Correlation Inertia Proportion
Dimension 1 .459 .211 .933
Dimension 2 .008 .000 .000
Standard coordinates:
Dimension 1 Dimension 2
I like them: AAPT/Cellular One - No -.52 -.01
I like them: AAPT/Cellular One - Yes 3.09 .06
I like them: New Tel - No -.49 -.01
I like them: New Tel - Yes 3.56 .07
I like them: One-tel - No -.50 .00
I like them: One-tel - Yes 3.30 .01
I like them: Optus - No -.53 1.89
I like them: Optus - Yes .54 -1.92
I like them: Orange (Hutchison) - No -.57 .13
I like them: Orange (Hutchison) - Yes 1.62 -.36
I like them: Telstra (Mobile Net) - No -.53 .08
I like them: Telstra (Mobile Net) - Yes .85 -.12
I like them: Virgin Mobile - No -.56 -.07
I like them: Virgin Mobile - Yes 1.90 .24
I like them: Vodafone - No -.53 -2.11
I like them: Vodafone - Yes .52 2.04
Principal coordinates:
Dimension 1 Dimension 2
I like them: AAPT/Cellular One - No -.24 .00
I like them: AAPT/Cellular One - Yes 1.42 .00
I like them: New Tel - No -.23 .00
I like them: New Tel - Yes 1.63 .00
I like them: One-tel - No -.23 .00
I like them: One-tel - Yes 1.51 .00
I like them: Optus - No -.24 .01
I like them: Optus - Yes .25 -.02
I like them: Orange (Hutchison) - No -.26 .00
I like them: Orange (Hutchison) - Yes .74 .00
I like them: Telstra (Mobile Net) - No -.24 .00
I like them: Telstra (Mobile Net) - Yes .39 .00
I like them: Virgin Mobile - No -.26 .00
I like them: Virgin Mobile - Yes .87 .00
I like them: Vodafone - No -.24 -.02
I like them: Vodafone - Yes .24 .02
Cronbach's Alpha
Dimension 1 .87
Dimension 2 .06
The chart below shows the principal coordinates; note that the aspect ratio of this chart is greatly exaggerating the y-axis – if drawn so that the two axes were on the same scale, the y-axis would essentially disappear.
An alternative approach to analyzing this data is to select RAW DATA in the brown drop-down and run a traditional Correspondence Analysis.
Technical details
When performing multiple correspondence analysis, Q performs an adjustment of the inertias, as described in: Nenadic, O. and M. J. Greenacre (2005). "Computation of Multiple Correspondence Analysis, with Code in R." This correction does not guarantee that the resulting percentages add up to 100% as it is only an approximation.